As you may have noticed, there are a lot of dotted notes in music. What is their value? How long do you hold them for? How do you figure them out? There are probably a million questions like this running in your head every time you see one.
Right now, it may look very complicated to you. But, with a little math and some extra thinking, we are going to discover how you can problem solve any note with one dot next to them.
It is true that you can find double dotted notes and even triple dotted notes in music. That is a discussion for another time. Today, we are focusing on understanding the meaning behind one dot first.
To help us get started, we first need to talk about the dot rule.
Dot Rule
The dot rule states this: A dot adds half the value of the note to the note.
To problem solve a dotted note, here are 3 steps to follow:
- Figure out the value of the note the dot is attached to.
- Decide what half the value of the note is. This amount represents the dot.
- Add the value of the dot to the value of the note.
Let’s put this into practice by using an example. Take a look at this dotted half note. 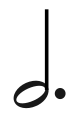 As you can see, the dot is attached to a half note.
As you can see, the dot is attached to a half note.
Step 1: How many counts are half notes again? Yes, they are worth 2 counts. Good, that was the first thing that we needed to establish.
Step 2: The next thing we need to do is find out what half the value of a half note is. What do you think? When you slice a half note in half (divide it by 2), half the value of a half note is equal to 1. That 1 represents the value of the dot. It might be helpful to remember that two quarter notes equal one half note.
Step 3: Now, we are going to add 1 (value of the dot) to the half note (value of 2 counts).
Final Result: A dotted half note is equal to 3 counts.
That was easy enough wasn’t it? Let’s practice this a little bit more on some other kinds of dotted notes.
More Practice
Take a look at the dotted whole note.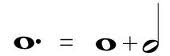
Step 1: How many counts are whole notes? Yes, they are 4 counts total.
Step 2: Divide the whole note in half. What do you get? The answer should be 2 counts (4 divided by 2 = 2). This means the value of the dot equals 2. If you remember, 2 half notes equal one whole note.
Step 3: Add the whole note to the dot. (4 + 2 = 6)
Final Result: A dotted whole note equals 6 counts.
Let’s do one more. How about a dotted quarter note?
Step 1: How many counts is a quarter note? Quarter notes are worth 1 count total.
Step 2: If we divide the quarter by 2 (or slice it in half), what do you get? Yes, you get 1/2. (1 divided by 2 = 1/2) Keep in mind that 1 quarter note equals 2 eighth notes. One half of a quarter note is equal to just one single eighth note. The dot, therefore, equals 1/2.
Step 3: Add the quarter note value to the dot value. (1 + 1/2 = 1 1/2).
Final Result: The total value of a dotted quarter note equals 1 1/2. That may seem odd, but we will learn more about dotted quarter notes later to understand where the other 1/2 count will come from to complete the rhythm.
Q & A
Q: Does the dot rule apply to rests also?
A: Yes it does. The only difference between a rest and a note is one represents sound (note) while the other represents silence (rest). Apply the same 3 steps above and you will get the correct result.
In Conclusion
Dotted notes in music really don’t have to be a stumbling block. Using these 3 easy steps will help you problem solve them every time. With enough practice using some simple math, you will become an expert at solving any note with one dot attached to it.

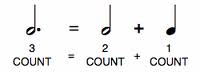
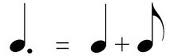
Hi Teresa,
Thank you for your site.
I have a specific question about Scott Joplin’s rag “Solace”.
The F Clef begins with two dotted low G notes.
That is, Dotted eighth note Low G to sixteenth G below middle C.
The next beat is an eighth chord and an eighth note.
Simple enough to understand. However, the beginning dotted Low G has another dotted Low G right next to it.
I do not understand this rhythm and cannot hear it from the various recordings.
I’ve tried guessing and don’t want to confuse the issue.
If you could answer this for me, I would be extremely grateful.
Thank you very much.
Hi Dennis,
From the description you have given, it may be a misprint in the music. Here’s a copy of Joplin’s “Solace” to look at for reference: http://www.sheetmusicplus.com/title/Solace/3700527#
Starting in measure 5, the rhythm in the bass clef is consistently a dotted eighth note followed by a sixteenth note on count 1 with two eighth notes on count 2. I like to count this as “1-(e-&)a-2-&”. I do not see the first dotted Low G having another dotted Low G next to it in this edition. This may be why you are not able to hear it in different recordings.
Compare your copy with other various editions online. The editors/publishers may have made a mistake in the music. Finding editorial mistakes in music is not as uncommon as you might think, especially in more difficult pieces like this.
Please let me know how else I can be of assistance. Thanks so much for stopping by and asking a really great question!
Hi Teresa,
You’re a godsend.
You are right, I misrepresented the first note in measure five. In fact I didn’t even mention measure five. Thank you for your understanding.
I agree with your assessment of (online) measure five–almost.
I was practicing this piece over the weekend and it occurred to me that
1) I was wrong about the note value.
2) Unless you can really work out the fingering, only ginormous man-hands can play it as written.
In measure 5, (online) the 8th note shares a downward stem with a quarter note.
I propose that the true value of the note is a dotted quarter which means it would be held until the final sixteenth note is played.
The final note being an 8th by the tagged stem and a sixteenth because of the flag.
I have the Schirmer’s Complete Joplin Rags which is printed to make the reading easier-once it’s decoded. The first note is tagged upward followed immediately by the dotted quarter. This is strange, but was probably widely accepted at the time of publication.
Crazy as this seems, in measure 6, one would have to hold down the first note while making an almost two octave stretch to hit the chord–OR–try a tenth interval with the right hand!
If I’m right, I wonder how either of those moves could be taught.
This is my best guess.
I never would have even considered making it if it weren’t for you and your really fine site.
I’d be very grateful for your thoughts.
Thank you
Dennis
Hi Dennis,
Basically what your theory is in how to play the music is correct. It takes a little bit deeper music theory and music history to fully understand it. That really is not absolutely necessary to enjoy the music. I just find it fun!
Don’t let the downward stems throw you off. There is actually 3 different lines (not just 2) of music happening at once in that measure. The sixteenth notes in the treble clef is one line, the stems up dotted eighth note to sixteenth and two eighth notes is the second line, and the stems down dotted quarter note followed by a single eighth note is the third line.
This is modeled after the Baroque period polyphonic music writing. There is no harmony, just multiple melody lines all happening at the same time (horizontally). Joplin did throw in a few chords to add a little homophonic (chordal) richness and texture.
Technically, the way you are supposed to play this measure is to hold the dotted quarter note in your left hand pinkie (finger 5) while playing the rest of the notes in the measure. There is no use of pedal here to help out holding that first note. You must hold it with your 5th finger only. You are right about measure 6. This would be virtually impossible! You will have to lift your hand to play the notes that follow. I think that is what Joplin intended anyways (even though he did have monster-size hands!). This is not a lyrical piece where everything sounds smooth and connected. This is a percussive piece where notes should sound slightly detached and light.
Ragtime music was invented due to a need for 1 musician to replace the sound of a full band. During the depression, no one could hire a band to play anymore. Joplin needed a job, so he created the ragtime sound mimicking a full a band! Pretty clever! If you can’t find a job, create one!
Well, that’s just a few of my thoughts. I hope it helps! By the way, thanks for all the kind compliments!